Rangkuman Materi Persamaan Garis Lurus Matematika SMP/MTs Kelas VIII Kurikulum 2013
Friday, October 25, 2019
matematika,
Matematika Kelas 8,
Matematika SMP/MTs Kelas 8,
Persamaan Garis Lurus
Edit
Bismillah....
Bentuk umum :
y = mx + c
dimana:
m = gradien (kemiringan garis)
c = konstanta
Untuk mencari nilai gradien suatu garis dapat dilakukan dengan beberapa cara yaitu:
1. Garis melalui dua titik (x1, y1) dan (x2, y2)
contoh soal:
gradien garis lurus yang melalui titik (5,2) dan (-1,8) adalah....

2. Garis melalui pusat koordinat 0 dan melalui titik (x1, y1)
contoh:
Gradien garis lurus melalui titik (0,0) dan (4,8) adalah....
Jawab:
m = y1/x1 ? x1= 4 ; y1= 8
= 8/4 = 2
3. Garis memotong kedua sumbu
a. Garis miring ke kanan
b. Garis miring ke kiri
4. Persamaan garis ax + by + c = 0 maka
contoh:
Gradien garis dengan persamaan 2x � y - 5 = 0 adalah...
Jawab:
2x � y - 5 = 0 ? ax + by + c = 0, maka a = 2 ; b = -1 dan c = -5
5. Garis sejajar sumbu x
contoh:
Gradien garis y = 4 adalah....
jawab:
y = mx + c ? y = 0x + 4
dijadikan ke bentuk persamaan ax + by + c = 0 menjadi
0x � y + 4 = 0 ? a = 0 ; b = -1
6. Garis sejajar sumbu y
contoh:
gradien garis x = 2 adalah....
Jawab:
y = mx + c ? mx = y � c ? x = 0y + 2
dijadikan ke bentuk persamaan ax + by + c = 0 menjadi
x � 0y - 2 = 0 ? a = 1; b = 0
Persamaan garisnya :
2. Persamaan garis yang melalui titik (0,c) dan bergradien m
Persamaan garisnya:
3. Persamaan garis yang melalui titik (x1, y1) dan bergradien m
contoh:
persamaan garis lurus melalui titik (5,10) dan bergradien 2 adalah...
Jawab:
Persamaan garisnya:
y � y1 = m(x - x1) ? m = 2 ; x1= 5 ; y1 = 10
y � 10 = 2 (x - 5)
y � 10 = 2x � 10
y = 2x � 10 + 10
y = 2x
4. Persamaan garis yang melalui titik (x1, y1) dan (x2, y2)
contoh:
Persamaan garis lurus melalui titik (2,4) dan (-3,-2) adalah....
Jawab:
persamaan garisnya:
2(y+3) = x � 2
2y + 6 = x � 2
2y = x � 2 � 6
2y = x � 8
5. Persamaan garis yang memotong sumbu x dan sumbu y di titik (x1, 0) dan (0,y1)
contoh:
Persamaan garis lurus melalui titik (4,0) dan (0,8) adalah....
Jawab:
persamaan garisnya:
y1. x + x1. y = x1. y1 ? x1 = 4 dan y1 = 8
8x + 4y = 4 . 8
8x + 4 y = 32
2x + y = 8
y = 8 � 2x
gradien dua garis lurus adalah sama
Garis a sejajar dengan garis b.
Jika gradien garis a = ma dan
b gradien garis b = mb , maka
ma = mb
Persamaan garis yang sejajar dengan garis ax + by + c = 0 dan melalui titik (x1, y1) adalah ax + by = ax1+ by1
contoh :
Persamaan garis yang melalui titik (2,3)dan sejajar dengan garis 3x+5y � 15 = 0 adalah...
Jawab:
cara1:
cari gradien garis 3x+5y � 15 = 0 ? 5y= -3x + 15
y = -3/5 x + 3 ? gradiennya = m= -3/5
Karena sejajar maka persamaan garis yang dicari gradiennya adalah sama.
Persamaan garis yang melalui titik (2,3) dengan gradien m = -3/5 adalah
y � y1 = m(x - x1) ? x1 = 2 ; y1 = 3
y � 3 = -3/5 (x � 2)
y � 3 = -3/5 x + ? 6/5dikali 5
5y � 15 = -3x + 6
3x + 5y = 21
cara2:
Persamaan garis yang sejajar dengan garis ax + by + c = 0 dan melalui titik (x1, y1)
adalah ax + by = ax1+ by1
Garis 3x+5y � 15 = 0, melalui titik (2,3)
a = 3 ; b = 5 ; x1 = 2 ; y1 = 3
Persamaan garisnya:
3x + 5y = 3 . 2 + 5 . 3
3x + 5y = 21
2. Gradien dua garis tegak lurus
Persamaan garis yang tegak lurus dengan garis ax + by + c = 0 dan melalui titik (x1, y1) adalah ay - bx = ay1 � bx1
contoh:
Persamaan garis lurus melalui titik (3,5) dan tegak lurus garis 2x + y � 5 = 0
adalah...
Jawab:
Cara1:
Ditentukan dulu gradien garis 2x + y � 5 = 0
y = -2x + 5 ? gradiennya = m = -2
Cara2:
Persamaan garis yang tegak lurus dengan garis ax + by + c = 0 dan melalui titik (x1, y1) adalah ay - bx = ay1 � bx1
Garis 2x + y � 5 = 0 melalui titik (3,5) adalah a = 2 ; b=1 ; x1 = 3 ; y1 = 5
Persamaan garisnya
2y � x = 2 . 5 � 1. 3
2y � x = 7
1. Substitusi
Dengan memasukkan salah satu varibel dari persamaan yang satu ke persamaan
yang lain.
2. Eliminasi
Dengan mengeliminasi (menghilangkan) salah satu variabel dengan cara
menyamakan variabel yang akan dieliminasi.
contoh:
Tentukan titik potong garis 2x + y � 6 = 0 dengan garis 2y � x - 7 = 0
Jawab:
Cara 1 (substitusi):
2x + y � 6 = 0 ...(1)
2y � x - 7 = 0 ? x = 2y � 7 ..(2)
Substitusi (2) ke (1)
2 (2y-7) + y � 6 = 0
4y � 14 + y � 6 = 0
5y � 20 = 0
5y = 20
y = 4
masukkan nilai y ke (1) lagi:
2x + 4 � 6 = 0
2x � 2 = 0
2x = 2
x = 1
diperoleh titik potongnya adalah (1,4)
Cara 2 (eliminasi):
2x + y � 6 = 0
2y � x - 7 = 0 ? x � 2y + 7 = 0
masukkan y = 4 :
2 . 4 � x � 7 = 0
8 � x � 7 = 0
1 � x = 0
x = 1
didapat titik potong (1,4)
Demikian ulasan tentang rangkuman materi matematika SMP/MTs K13 yaitu tentang Persamaan Garis Lurus. Terimakasi sudah berkunjung dan semoga bermanfaat.
Sahabat baiq yang berbahagia. Kali ini kembali saya akan berbagi materi matematika SMP/MTs Kelas VIII Kurikulum 2013 yaitu tentang Persamaan Garis Lurus. Adapun materi Matematika SMP/MTs Kelas VIII sebelumnya yang telah saya posting adalah tentang Sistem Koordinat Cartesius serta Relasi dan Fungsi/Pemetaan dan bagi yang belum mempelajarinya silahkan bisa klik DISINI.
Baiklah kali ini langsung saja kita pelajari materi matematika SMP/MTs kelas 8 yaitu tentang Persamaan Garis Lurus. Semangat dan Selamat belajar!A. Pengertian Pesamaan Garis Lurus
Persamaan garis lurus adalah suatu fungsi yang apabila digambarkan ke dalam bidang Cartesius akan berbentuk garis lurus. Garis lurus ini mempunyai nilai kemiringan suatu gris yang dinamakan gradien (m).Bentuk umum :
y = mx + c
dimana:
m = gradien (kemiringan garis)
c = konstanta
B. Gradien Garis Lurus (m)
Gradien adalah nilai yang menyatakan kemiringan suatu garis yang dinyatakan dengan m.Untuk mencari nilai gradien suatu garis dapat dilakukan dengan beberapa cara yaitu:
1. Garis melalui dua titik (x1, y1) dan (x2, y2)
contoh soal:
gradien garis lurus yang melalui titik (5,2) dan (-1,8) adalah....

2. Garis melalui pusat koordinat 0 dan melalui titik (x1, y1)
contoh:
Gradien garis lurus melalui titik (0,0) dan (4,8) adalah....
Jawab:
m = y1/x1 ? x1= 4 ; y1= 8
= 8/4 = 2
3. Garis memotong kedua sumbu
a. Garis miring ke kanan
b. Garis miring ke kiri
4. Persamaan garis ax + by + c = 0 maka
contoh:
Gradien garis dengan persamaan 2x � y - 5 = 0 adalah...
Jawab:
2x � y - 5 = 0 ? ax + by + c = 0, maka a = 2 ; b = -1 dan c = -5
5. Garis sejajar sumbu x
contoh:
Gradien garis y = 4 adalah....
jawab:
y = mx + c ? y = 0x + 4
dijadikan ke bentuk persamaan ax + by + c = 0 menjadi
0x � y + 4 = 0 ? a = 0 ; b = -1
6. Garis sejajar sumbu y
contoh:
gradien garis x = 2 adalah....
Jawab:
y = mx + c ? mx = y � c ? x = 0y + 2
dijadikan ke bentuk persamaan ax + by + c = 0 menjadi
x � 0y - 2 = 0 ? a = 1; b = 0
C. Menentukan Persamaan Garis Lurus
1. Persamaan garis yang melalui titik O (0,0) dan bergradien m.Persamaan garisnya :
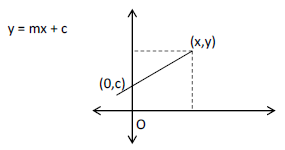
2. Persamaan garis yang melalui titik (0,c) dan bergradien m
Persamaan garisnya:
3. Persamaan garis yang melalui titik (x1, y1) dan bergradien m
contoh:
persamaan garis lurus melalui titik (5,10) dan bergradien 2 adalah...
Jawab:
Persamaan garisnya:
y � y1 = m(x - x1) ? m = 2 ; x1= 5 ; y1 = 10
y � 10 = 2 (x - 5)
y � 10 = 2x � 10
y = 2x � 10 + 10
y = 2x
4. Persamaan garis yang melalui titik (x1, y1) dan (x2, y2)
contoh:
Persamaan garis lurus melalui titik (2,4) dan (-3,-2) adalah....
Jawab:
persamaan garisnya:
2(y+3) = x � 2
2y + 6 = x � 2
2y = x � 2 � 6
2y = x � 8
5. Persamaan garis yang memotong sumbu x dan sumbu y di titik (x1, 0) dan (0,y1)
contoh:
Persamaan garis lurus melalui titik (4,0) dan (0,8) adalah....
Jawab:
persamaan garisnya:
y1. x + x1. y = x1. y1 ? x1 = 4 dan y1 = 8
8x + 4y = 4 . 8
8x + 4 y = 32
2x + y = 8
y = 8 � 2x
D. Hubungan antara dua Garis Lurus
1. Gradien dua garis sejajargradien dua garis lurus adalah sama
Garis a sejajar dengan garis b.
Jika gradien garis a = ma dan
b gradien garis b = mb , maka
ma = mb
Persamaan garis yang sejajar dengan garis ax + by + c = 0 dan melalui titik (x1, y1) adalah ax + by = ax1+ by1
contoh :
Persamaan garis yang melalui titik (2,3)dan sejajar dengan garis 3x+5y � 15 = 0 adalah...
Jawab:
cara1:
cari gradien garis 3x+5y � 15 = 0 ? 5y= -3x + 15
y = -3/5 x + 3 ? gradiennya = m= -3/5
Karena sejajar maka persamaan garis yang dicari gradiennya adalah sama.
Persamaan garis yang melalui titik (2,3) dengan gradien m = -3/5 adalah
y � y1 = m(x - x1) ? x1 = 2 ; y1 = 3
y � 3 = -3/5 (x � 2)
y � 3 = -3/5 x + ? 6/5dikali 5
5y � 15 = -3x + 6
3x + 5y = 21
cara2:
Persamaan garis yang sejajar dengan garis ax + by + c = 0 dan melalui titik (x1, y1)
adalah ax + by = ax1+ by1
Garis 3x+5y � 15 = 0, melalui titik (2,3)
a = 3 ; b = 5 ; x1 = 2 ; y1 = 3
Persamaan garisnya:
3x + 5y = 3 . 2 + 5 . 3
3x + 5y = 21
2. Gradien dua garis tegak lurus
Persamaan garis yang tegak lurus dengan garis ax + by + c = 0 dan melalui titik (x1, y1) adalah ay - bx = ay1 � bx1
contoh:
Persamaan garis lurus melalui titik (3,5) dan tegak lurus garis 2x + y � 5 = 0
adalah...
Jawab:
Cara1:
Ditentukan dulu gradien garis 2x + y � 5 = 0
y = -2x + 5 ? gradiennya = m = -2
Cara2:
Persamaan garis yang tegak lurus dengan garis ax + by + c = 0 dan melalui titik (x1, y1) adalah ay - bx = ay1 � bx1
Garis 2x + y � 5 = 0 melalui titik (3,5) adalah a = 2 ; b=1 ; x1 = 3 ; y1 = 5
Persamaan garisnya
2y � x = 2 . 5 � 1. 3
2y � x = 7
E. Menentukan titik potong dari dua garis lurus
Titik potong dari dua garis lurus dapat dilakukan dengan 2 cara:1. Substitusi
Dengan memasukkan salah satu varibel dari persamaan yang satu ke persamaan
yang lain.
2. Eliminasi
Dengan mengeliminasi (menghilangkan) salah satu variabel dengan cara
menyamakan variabel yang akan dieliminasi.
contoh:
Tentukan titik potong garis 2x + y � 6 = 0 dengan garis 2y � x - 7 = 0
Jawab:
Cara 1 (substitusi):
2x + y � 6 = 0 ...(1)
2y � x - 7 = 0 ? x = 2y � 7 ..(2)
Substitusi (2) ke (1)
2 (2y-7) + y � 6 = 0
4y � 14 + y � 6 = 0
5y � 20 = 0
5y = 20
y = 4
masukkan nilai y ke (1) lagi:
2x + 4 � 6 = 0
2x � 2 = 0
2x = 2
x = 1
diperoleh titik potongnya adalah (1,4)
Cara 2 (eliminasi):
2x + y � 6 = 0
2y � x - 7 = 0 ? x � 2y + 7 = 0
masukkan y = 4 :
2 . 4 � x � 7 = 0
8 � x � 7 = 0
1 � x = 0
x = 1
didapat titik potong (1,4)
Demikian ulasan tentang rangkuman materi matematika SMP/MTs K13 yaitu tentang Persamaan Garis Lurus. Terimakasi sudah berkunjung dan semoga bermanfaat.
Baca Juga:
- Rangkuman Materi Matematika SMP/MTs Kelas VII K13
- Rangkuman Materi Matematika SMP/MTs Kelas VIII K13
- Rangkuman Materi Sistem Koordinat Cartesius SMP/MTs


















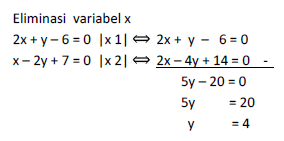
0 Response to "Rangkuman Materi Persamaan Garis Lurus Matematika SMP/MTs Kelas VIII Kurikulum 2013"
Post a Comment